函数与导数部分的题型梳理
题型解法
函数与导数部分是现行高考制度下的压轴题目,学生一般就做到第21题的第一问,第二问是留给学有余力的学生做的,所以大多数学生的关注点应该在第一问上,现将第一问的常见考法和题型做以梳理如下:
【类型①】求函数的切线问题,
解法思路:在点处,利用点斜式求解;过点处设切点,求出切点及斜率;
解析:设直线\(y=kx+b\)与函数\(C_0:y=lnx+2\)相切于点\(P_0(x_0,y_0)\),
直线\(y=kx+b\)与函数\(C_1:y=ln(x+1)\)相切于点\(P_1(x_1,y_1)\),
则由题可知,在点\(P_0(x_0,y_0)\)处的切线方程为\(y-y_0=f'(x_0)(x-x_0)\),
即\(y-(lnx_0+2)=\cfrac{1}{x_0}(x-x_0)\),
化简为\(y=\cfrac{1}{x_0}x+lnx_0+1\);
同理同法,点\(P_1(x_1,y_1)\)处的切线方程为\(y-y_1=f'(x_1)(x-x_1)\),
即\(y-ln(x_1+1)=\cfrac{1}{x_1+1}(x-x_1)\),
化简为\(y=\cfrac{1}{x_1+1}x+ln(x_1+1)-\cfrac{x_1}{x_1+1}\)
由这两条切线是同一条可知【同一法】,
\(\begin{cases} k=\cfrac{1}{x_0}=\cfrac{1}{x_1+1} \\ b=lnx_0+1=ln(x_1+1)-\cfrac{x_1}{x_1+1} \end{cases}\)
解得:\(\begin{cases} x_0=x_1+1 \\ x_0=\cfrac{1}{2},x_1=-\cfrac{1}{2}\end{cases}\)
所以\(b=1+lnx_0=1+ln(\cfrac{1}{2})=1-ln2\)。
分析:利用点斜式来求解,
其中斜率\(k=f'(x)_{|x=1}=(2x-\cfrac{1}{x^2})_{|x=1}=1\),
切点是\((1,2)\),
故切线方程为\(y-2=1(x-1)\),整理为\(y=x+1\)。
3、公切线问题,常考虑用同一法。
4、牢记下边这个模型:
【等价题目】直线\(y=x\)上的点为\(P(x,y)\),函数\(y=lnx\)上的点是\(Q(m,n)\),求\(\sqrt{(x-m)^2+(y-n)^2}\)的最小值。
思路:平行线法,
设和直线\(y=x\)平行且和函数\(y=lnx\)相切的直线为\(y=x+m\),
切点为\(P_0(x_0,y_0)\),则有
\(\begin{cases} y_0=x_{0}+ m \\ y_0=lnx_0 \\ f'(x_0)=\cfrac{1}{x_0}=1\end{cases}\);
从而解得\(x_0=1,y_0=0,m=-1\)
所以所求的点点距的最小值,就转化为切点\(P_0(1,0)\)到直线\(y=x\)的点线距,
或者两条直线\(y=x,y=x-1\)的线线距了。
【类型②】利用导函数的方程组,求解函数中的参数;进一步求函数的单调性。解法思路:求解方程(组),解不等式。
分析:由题目可知,\(f'(x)=\cfrac{ax-(ax+b)}{x^2}e^x+\cfrac{ax+b}{x}e^x\)
\(f'(-1)=0,f(-1)=\cfrac{1}{e}\),
分别求得\(a-2b=0\)和\(a-b=1\),联立求得\(a=2,b=1\);
则\(f(x)=\cfrac{2x+1}{x}\cdot e^x\);
求解单调区间,实质就是解不等式
\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}>0\)
和\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}<0\),
此时可以通过穿根法解分式不等式。
\((-\infty,-1)和(\cfrac{1}{2},+\infty)\)单调递增;\((-1,0)和(0,\cfrac{1}{2})\)单调递减;
【又例】【2017全国卷2文科第21题高考真题选编】设函数\(f(x)=(1-x^2)e^x\),讨论\(f(x)\)的单调性;
分析:本题目一般要借助导数工具来讨论单调性,
<img src="http://images2015.cnblogs.com/blog/992978/201707/992978-20170705140219112-1678749705.png" / >
\(f'(x)=-2xe^x+(1-x^2)e^x=(-x^2-2x+1)e^x\),由于\(e^x\)的值恒为正,
【思路提示:此时我们只要能做出导函数的其中一部分\(-x^2-2x+1=g(x)\)的图像,结合图像就能讨论单调性】
令\(-x^2-2x+1=0\),得到\(x=\pm\sqrt{2}-1\),且二次函数\(g(x)\)的开口向下,
如图所示,故有以下结论
当\(x<-\sqrt{2}-1\)时,\(f'(x)<0\),\(f(x)\)单调递减;
当\(-\sqrt{2}-1< x<\sqrt{2}-1\)时,\(f'(x)>0\),\(f(x)\)单调递增;
当\(x>\sqrt{2}-1\)时,\(f'(x)<0\),\(f(x)\)单调递减;
故可得到函数\(f(x)\)的单调递减区间是\((-\infty,-\sqrt{2}-1)\)和\((\sqrt{2}-1,+\infty)\);
单调递增区间是\((-\sqrt{2}-1,\sqrt{2}-1)\)。
感悟反思:1、注意,题目中的一句话中的多个信息点,比如函数\(f(x)\)在\(x=1\)处取到极值3,则必有关系式\(\begin{cases}f'(1)=0\\f(1)=3\end{cases}\);2、同时注意复合函数的导数的求法,比如\(f(x)=ln(2x-1)\),则\(f'(x)=\cfrac{1}{2x-1}\cdot (2x-1)'=\cfrac{2}{2x-1}\),千万不要出错了。3、注意积的导数法则和商的导数法则,很容易出错的。4、注意解不等式的方法,如穿根法,以及利用导函数的部分图像来确定整个导数的正负的技巧。
【类型③】已知含字母参数的函数,求其单调区间,解法思路:求解对应的含参不等式,常常需要分类讨论;
分析:利用导数求导解决,
\(f'(x)=e^x(e^x-a)+e^x\cdot e^x-a^2=2e^{2x}-e^xa-a^2=(e^x-a)(2e^x+a)\),
以下针对\(a\)分类讨论如下: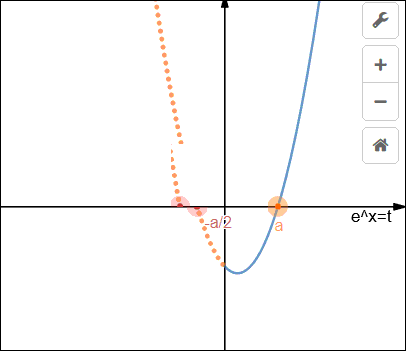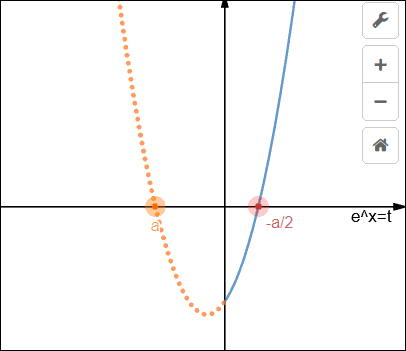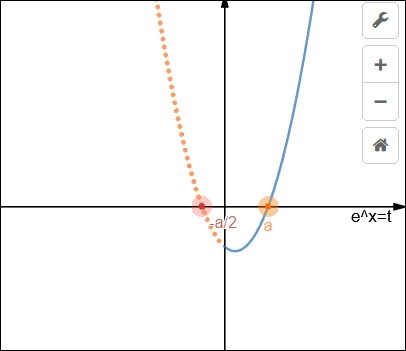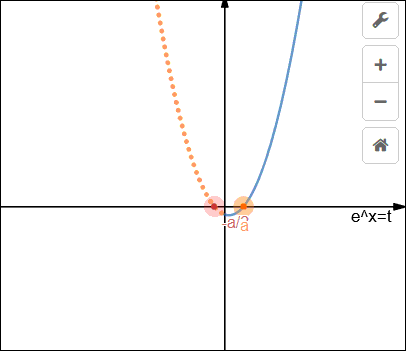
当\(a=0\)时,\(f'(x)>0\)恒成立,\(f(x)\)在区间\((-\infty,+\infty)\)上单调递增。
当\(a>0\)时,令$ e^x>a \(,解得\)x>lna$,
$ f'(x)>0 \(,即在区间\)(lna,+\infty)\(上函数\)f(x)$单调递增;
令$ e^x < a \(,解得\)x < lna $,
\(f'(x)<0\),即在区间\((-\infty,lna)\)上函数\(f(x)\)单调递减;
当\(a<0\)时,令\(e^x>-\cfrac{a}{2}\),解得\(x>ln(-\cfrac{a}{2})\),
\(f'(x)>0\),即在区间\((ln(-\cfrac{a}{2}),+\infty)\)上函数\(f(x)\)单调递增;
令\(e^x<-\cfrac{a}{2}\),解得\(x < ln(-\cfrac{a}{2})\),\(f'(x)<0\),
即在区间\((-\infty,ln(-\cfrac{a}{2}))\)上函数\(f(x)\)单调递减;
综上所述,
当\(a<0\)时,函数\(f(x)\)的单减区间是\((-\infty,ln(-\cfrac{a}{2}))\),单增区间是\((ln(-\cfrac{a}{2}),+\infty)\);
当\(a=0\)时,单增区间是\((-\infty,+\infty)\),无单减区间;
当\(a>0\)时,函数\(f(x)\)的单减区间是\((-\infty,lna)\),单增区间是\((lna,+\infty)\);
令\(g(x)=f'(x)\),求\(g(x)\)的单调区间;
解析:\(g(x)=f'(x)= lnx-2ax+2a,x\in (0,+\infty)\)
则\(g'(x)= \cfrac{1}{x}-2a=\cfrac{1-2ax}{x}\)
\(1^。\)当\(a\leq 0\)时,\(x\in(0,+\infty)\),\(g'(x)>0,g(x)\nearrow\)
\(2^。\)当\(a> 0\)时,令\(g'(x)=0,1-2ax=0,x=\cfrac{1}{2a}\)
当\(x\in (0,\cfrac{1}{2a})\),\(g'(x)>0,g(x)\nearrow\);
当\(x\in (\cfrac{1}{2a},+\infty)\),\(g'(x)<0,g(x)\searrow\);
综上所述,
当\(a\leq 0\)时,单增区间为\((0,+\infty)\),无单减区间;
当\(a> 0\)时,单增区间为\((0,\cfrac{1}{2a})\),单减区间为\((\cfrac{1}{2a},+\infty)\)。
(1) 讨论函数\(f(x)\)的单调性。
分析:先求定义域得\((0,+\infty)\),求导得到\(f'(x)=\cfrac{a+1}{x}+2ax=\cfrac{2ax^2+a+1}{x}\),
然后只考虑分子函数\(g(x)=2ax^2+a+1\)的图像,
先考虑\(a=0\),在考虑函数\(g(x)\)图像恒在\(x\)轴上方,恒在\(x\)轴下方,以及\(x\)轴上方下方都有图像的情形,
自然就得到了分类的标准有\(a=0\),\(a>0\),\(a+1\leq 0\),以及\(-1< a<0\),在解答时做一综合就行了。
解:当\(a\ge 0\)时,\(g(x)>0\)恒成立,则\(f'(x)=\cfrac{2ax^2+a+1}{x}>0\),故\(f(x)\)在\((0,+\infty)\)上单调递增;
当\(a\leq -1\)时,\(g(x)\leq 0\)恒成立,则则\(f'(x)=\cfrac{2ax^2+a+1}{x}<0\),故\(f(x)\)在\((0,+\infty)\)上单调递减;
当\(-1< a<0\)时,令\(f'(x)=0\),解得\(x=\sqrt{-\cfrac{a+1}{2a}}=x_0\),即\(x\in(0,x_0)\)时,\(f'(x)>0\),
故\(f(x)\)在\((0,x_0)\)上单调递增;\(x\in(x_0,+\infty)\)时,\(f'(x)<0\),故\(f(x)\)在\((x_0,+\infty)\)上单调递减;
感悟反思:1、涉及分类讨论的题目,务必要注意分类标准的唯一性,要做到不重复不遗漏。2、务必想到借助导函数的图像或者其分子图像或者其部分图像,来确定导函数的正负,这体现了以形助数的思维特点。
【类型④】利用导数求函数的极值。
解法思路:利用导数先分析单调性,从而得到函数的极值;
A、-1 \(\hspace{2cm}\) B、\(-2e^{-3}\) \(\hspace{2cm}\) C、\(e^{-3}\) \(\hspace{2cm}\) D、 1
分析:\(f'(x)=(2x+a)e^{x-1}+(x^2+ax-1)e^{x-1}=e^{x-1}[x^2+(a+2)x+a-1]\),
又由题目可知\(f'(-2)=0\),即\(f'(-2)=e[4+(a+2)(-2)+a-1]=0\),解得\(a=-1\)
故原函数\(f(x)=(x^2-x-1)e^{x-1}\),
其导函数\(f'(x)=e^{x-1}(x^2+x-2)=e^{x-1}(x+2)(x-1)\),
仿照上例,做出函数\(g(x)=(x+2)(x-1)\)的图像可知,
函数的极小值点是\(x=1\);
故函数\(f(x)_{极小}=f(1)=-1\)。故选A。
感悟反思:1、注意定义域优先的原则;2、此时我们常常借助导函数的图像或者导函数的分子图像,来简化判断导函数的正负。这体现了数形结合的数学思想。也体现了学以致用的数学方向。3、极值点\(x_0\)应该是导函数\(f'(x)\)的变号零点,如果是不变号零点,这一点不能成为极值点。
【类型⑤】求数字系数的函数的最值;解法思路:先求单调性,由单调性再求极值,添加端点值后比较,得到最值
解析:由题目可知,定义域为\((0,+\infty)\);
当\(a=-4\;\)时,\(f'(x)=\cfrac{-4}{x}+2x=\cfrac{2x^2-4}{x}=\cfrac{2(x-\sqrt{2})(x+\sqrt{2})}{x}\)
借助导函数的分子的图像和\(x\in [1,e]\),
可知\(x\in[1,\sqrt{2})\)时,\(f'(x)<0,f(x)\searrow\);
\(x\in(\sqrt{2},e]\)时,\(f'(x)>0,f(x)\nearrow\);
又因为端点值\(f(1)=1,f(e)=e^2-4>f(1)\),
故\(x=e\)时,\(f(x)_{max}=f(e)=e^2-4\)。
感悟反思:1、此时我们常常借助导函数的图像或者导函数的分子图像,来简化判断导函数的正负。这体现了数形结合的数学思想。也体现了学以致用的数学方向。2、注意定义域优先的原则。
【类型⑥】已知函数的极值,求参数的取值范围;解法思路:先用导数讨论分析函数的单调性,再针对极值分类讨论;
(1)分析函数的单调性;
(2)已知\(f(x)\)在\(x=1\)处取得极大值,求正实数\(a\)的取值范围.
解析:⑴\(g(x)=f'(x)= lnx-2ax+2a,x\in (0,+\infty)\)
则\(g'(x)= \cfrac{1}{x}-2a=\cfrac{1-2ax}{x}\)
\(1^。\)当\(a\leq 0\)时,\(x\in(0,+\infty)\),\(g'(x)>0,g(x)\nearrow\)
\(2^。\)当\(a> 0\)时,令\(g'(x)=0,1-2ax=0,x=\cfrac{1}{2a}\)
当\(x\in (0,\cfrac{1}{2a})\),\(g'(x)>0,g(x)\nearrow\);
当\(x\in (\cfrac{1}{2a},+\infty)\),\(g'(x)<0,g(x)\searrow\);
综上所述,
当\(a\leq 0\)时,单增区间为\((0,+\infty)\),无单减区间;
当\(a> 0\)时,单增区间为\((0,\cfrac{1}{2a})\),单减区间为\((\cfrac{1}{2a},+\infty)\)。
⑵ 由⑴知, 有\(f'(1)=0\)成立,
以下以定点1和动点\(\cfrac{1}{2a}\)的大小关系分类如下:
\(1^。\) 当 \(0 < a <\cfrac{1}{2}\)时,\(\cfrac{1}{2a}>1\),
由⑴知\(f'(x)\)在\((0,\cfrac{1}{2a})\)单增,
故\(x\in(0,1)\)时,\(f'(x)<0\),\(x\in(1,\cfrac{1}{2a})\)时,\(f'(x)>0\),
则函数\(f(x)\)在\(x=1\)处取得极小值,不符,舍去;
\(2^。\)当\(a=\cfrac{1}{2}\)时,\(\cfrac{1}{2a}=1\),\(f'(x)\)在\((0,1)\)上单增,在\((1,+\infty)\)上单减,
则\(x\in (0,+\infty)\)时,\(f'(x)\leq 0\),
故\(f(x)\searrow\),无极大值,不符,舍去;
\(3^。\)当\(a>\cfrac{1}{2}\)时,\(0<\cfrac{1}{2a}<1\),\(x\in(\cfrac{1}{2a},1)\)时,
\(f'(x)>0,f(x)\nearrow\),\(x\in(1,+\infty)\)时,\(f'(x)<0,f(x)\searrow\),
故在\(x=1\)处取到极大值,符合题意。
综上,\(a\in (\cfrac{1}{2},+\infty)\)。
感悟反思:1、此时我们常常借助导函数的图像或者导函数的分子图像,来简化判断导函数的正负。这体现了数形结合的数学思想。也体现了学以致用的数学方向。2、注意定义域优先的原则。
【类型⑦】讨论方程根的个数;解法思路:分离参数+恒成立+数形结合
解析:由题目可知,写出\(alnx+x^2=0\)时,我们很自然就想到是否可以分离参数,
此时需要考察参数\(a\)的系数\(lnx\)的正负,由\(x\in [1,e]\),
使得\(lnx\)有为零的可能性,故分类讨论如下:
当\(x=1\)时,方程\(f(x)=alnx+x^2=0\)无解;
当\(x>1\)时,\(lnx>0\),分离参数得到,
故方程\(f(x)=0\)的根的个数即就是方程\(-a=\cfrac{x^2}{lnx}\)的根的个数。
即函数\(g(x)=-a\)和函数\(h(x)=\cfrac{x^2}{lnx}\)的图像的交点个数。
又\(h'(x)=\cfrac{2xlnx-x^2\cdot\cfrac{1}{x}}{ln^2x}=\cfrac{x(2lnx-1)}{ln^2x}\),
借助导函数的分子的图像得到:
\(x\in(1,\sqrt{e})\)时,\(h'(x)<0,h(x)\searrow\);
\(x\in(\sqrt{e},e)\)时,\(h'(x)>0,h(x)\nearrow\);
又\(h(\sqrt{e})=2e,h(e)=e^2\),
到此我们应该手动就能画出函数的大致简图了。不过看看电脑作图。 课件链接
在同一个坐标系中作出函数\(g(x)\)和\(h(x)\)的图像可知,
\(1^。\)当\(-a<2e\)时,即\(a>-2e\)时,两个函数图像没有交点,原方程无解;
\(2^。\)当\(-a=2e\)时,即\(a=-2e\)时,两个函数图像有一个交点,原方程一个解;
\(3^。\)当\(2e<-a\leq e^2\)时,即\(-e^2\leq a<-2e\)时,两个函数图像有两个交点,原方程有两个解;
\(4^。\)当\(-a>e^2\)时,即\(a<-e^2\)时,两个函数图像有一个交点,原方程一个解;
综上所述,
当\(a>-2e\)时,原方程根的个数是0个;
当\(a<-e^2\)或\(a=-2e\)时,原方程根的个数是1个;
当\(-e^2\leq a<-2e\)时,原方程根的个数有2个;
【又例】(2016衡水金卷)已知函数\(f(x)=lnx-ax^2\),且函数\(f(x)\)在点\((2,f(2))\)处的切线的一个方向向量是\((2,-3)\).
(1)若关于\(x\)的方程\(f(x)+\cfrac{3}{2}x^2=3x-b\)在区间\([\cfrac{1}{2},2]\)上恰有两个不相等的实数根,求实数\(b\)的取值范围。
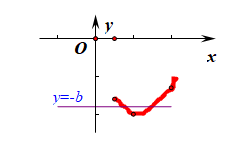
分析:\(f'(x)=\cfrac{1}{x}-2ax\),由函数\(f(x)\)在点\((2,f(2))\)处的切线的一个方向向量是\((2,-3)\),
即\(f'(2)=\cfrac{1}{2}-4a=-\cfrac{3}{2}\),解得\(a=\cfrac{1}{2}\),
方程\(f(x)+\cfrac{3}{2}x^2=3x-b\)变形为\(lnx+x^2-3x=-b\),
令\(g(x)=lnx+x^2-3x\),\(h(x)=-b\)。
\(g'(x)=\cfrac{(2x-1)(x-1)}{x}\),故函数\(g(x)\)在\((\cfrac{1}{2},1)\)上单调递减,在\((1,2)\)上单调递增,
又\(g(\cfrac{1}{2})=-ln2-\cfrac{5}{4}\),\(g(1)=-2\),\(g(2)=ln2-2\),
又\(g(\cfrac{1}{2})-g(2)=-2ln2+\cfrac{3}{4}<0\),故\(g(\cfrac{1}{2})< g(2)\),
在同一坐标系中作出函数\(g(x)\)和\(h(x)\)的大致图像如右,
由图可知要使两个函数有两个交点,则\(-2< b \leq -ln2-\cfrac{5}{4}\),
即\(ln2+\cfrac{5}{4}\leq b <2\),故\(b \in [\cfrac{5}{4}+ln2,2)\)。
感悟反思:1、能把题目顺利转化为恒成立问题。2、遇到恒成立命题求参数取值范围时,我们常常首选的方法是分离参数法,3、这个思路借助了数形结合的数学思想。
【类型⑧】已知函数在给定区间上的单调性,求参数的取值范围;
解法思路:或转化为集合的关系求解,或先转化为恒成立问题,再考虑分离参数求解;
⑵若对于任意的\(x\in (0,1)\),恒有\((1+x)\cdot f(x)+2a<0(a>0)\),求实数\(a\)的取值范围;
【解析】⑴由于\(f'(x)=\cfrac{\cfrac{1}{x}(1-x)+lnx}{(1-x)^2}\),
故\(\phi'(x)=(x-1)^2f'(x)=\cfrac{1}{x}(1-x)+lnx=\cfrac{1}{x}-1+lnx(x>0\&x\neq 1)\)
所以\(\phi'(x)=-\cfrac{1}{x^2}+\cfrac{1}{x}=\cfrac{x-1}{x^2}\),
则\(\phi(x)\)在区间\((0,1)\)单调递减,
又由题可知,函数\(\phi(x)\)在区间\((3m,m+\cfrac{1}{2})\)上单调递减,
则\((3m,m+\cfrac{1}{2})\subseteq (0,1)\),
则得到$ \begin{cases} 3m\ge 0 \ m+\cfrac{1}{2}\leq 1 \ 3m < m+\cfrac{1}{2} \end{cases}$。
则有$\begin{cases} m\ge 0 \ m < \cfrac{1}{4} \ m \leq \cfrac{1}{2} \end{cases} $,
解得\(0 \leq m < \cfrac{1}{4}\).
⑵转化为恒成立和分离参数来求解。
对于任意的\(x\in (0,1)\),恒有\(-2a\ge (1+x)\cdot f(x)\)成立,
令\(g(x)=(1+x)\cfrac{lnx}{1-x}\),
则\(g'(x)=\cfrac{lnx}{1-x}+(1-x)\cfrac{\cfrac{1}{x}(1-x)-lnx\cdot (1-x)'}{(1-x)^2}\)
\(=\cfrac{lnx}{1-x}+(1-x)\cfrac{\cfrac{1}{x}(1-x)+lnx}{(1-x)^2}\)
\(=\cfrac{lnx(1-x)+\cfrac{1}{x}(1-x)^2+(1+x)lnx}{(1-x)^2}=\cfrac{2lnx-x+\cfrac{1}{x}}{(1-x)^2}\),
再令\(h(x)=2lnx+\cfrac{1}{x}-x\),
则\(h'(x)=\cfrac{2}{x}-\cfrac{1}{x^2}-1\),
则\(h''(x)=-\cfrac{2}{x^2}+\cfrac{2}{x^3}=2(\cfrac{1}{x^3}-\cfrac{1}{x^2})>0\),
所以\(h'(x)\)在区间\((0,1)\)上单调递增,
又\(h'(1)=0\),则在区间\((0,1)\)上\(h'(x)<0\),
故\(h(x)\)在区间\((0,1)\)上单调递减,
又\(h(1)=0\),则在区间\((0,1)\)上\(h(x)>0\),
故在区间\((0,1)\)上\(g'(x)>0\),从而\(g(x)\)在区间\((0,1)\)上单调递增,
故\(g(x)_{max}= g(1)\),以下用洛必达法则求解\(g(1)\);
\(\lim\limits_{x\to 1} g(x)= \lim\limits_{x\to 1} \cfrac{((1+x)lnx)'}{(1-x)'}\)
\(=\lim\limits_{x\to 1} \cfrac{lnx+\cfrac{1+x}{x}}{-1}=-2\);
故\(g(x)_{max}= g(1)\),故\(-2a \ge -2\),又\(a>0\),解得\(0<a\leq 1\).
感悟反思:1、若函数的系数中不含参数,参数位置在给定区间上;解法思路:用常规方法求出单调区间,那么给定区间必然是求出的单调区间的子区间,转化为集合的关系求解;2、若参数包含在函数的系数中,给定区间里没有参数;解法思路:先转化为恒成立问题,再考虑分离参数求解;3、 洛必达法则
【类型⑨】已知函数的最值,求参数的取值范围;解法思路:先求单调性,由单调性得到最值,再结合其他条件得到等式或不等式求解
分析:(1)定义域为\((0,+\infty)\),又\(f'(x)=\cfrac{1}{x}-a=\cfrac{-ax+1}{x}\),
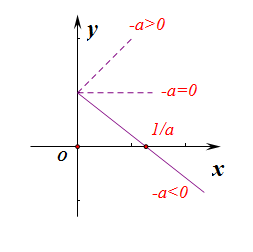
由于分母为正,故只针对分子\(-ax+1\)分类讨论,
当\(-a\ge 0\)时,即\(a\leq 0\)时,\(-ax+1>0\),即\(f'(x)>0\),故在\((0,+\infty)\)上单调递增;
当\(-a<0\)时,即\(a>0\)时,即令\(-ax+1=0\),得到\(x=\cfrac{1}{a}\),
当\(0<x<\cfrac{1}{a}\)时,\(f'(x)>0\),当\(x>\cfrac{1}{a}\)时,\(f'(x)<0\),
故在\((0,\cfrac{1}{a})\)上单调递增,在\((\cfrac{1}{a},+\infty)\)上单调递减;
综上,当\(a\leq 0\)时,在\((0,+\infty)\)上单调递增;
当\(a> 0\)时,在\((0,\cfrac{1}{a})\)上单调递增,在\((\cfrac{1}{a},+\infty)\)上单调递减;
(2)由(1)可知,当\(a \leq 0\)时,在\((0,+\infty)\)上单调递增,故无最大值;
当\(a> 0\)时,在\((0,\cfrac{1}{a})\)上单调递增,在\((\cfrac{1}{a},+\infty)\)上单调递减,
故在\(x=\cfrac{1}{a}\)处取到最大值,\(f(x)_{max}=f(\cfrac{1}{a})=ln\cfrac{1}{a}+a(1-\cfrac{1}{a})=-lna+a-1\),
由\(f(\cfrac{1}{a})>2a-2\)等价转化得到,\(lna+a-1<0\)。
以下求解不等式\(lna+a-1<0\)。可以有两个思路:
思路1:从形的角度入手,数形结合,先变形为\(lna<1-a\),做出两个函数\(y=lna\)和\(y=1-a\)的图像,如右图所示,
从图上观察可知,当\(a=1\)时\(lna=1-a\),当\(a>1\)时\(lna>1-a\),当\(0< a<1\)时\(lna < 1-a\),
故\(0< a<1\),再结合前提条件\(a >0\),得到\(a\)的取值范围为\((0,1)\)。
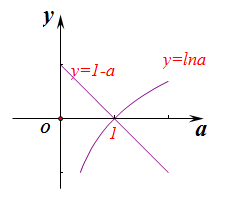
思路2:从数的角度,利用函数计算,令\(g(a)=lna+a-1(a>0)\),
则\(g'(a)=\cfrac{1}{a}+1>0\)恒成立,故\(g(x)\)在\((0,+\infty)\)上单调递增,
又\(g(1)=0\),故\(0< a<1\)时,\(g(a)<0\),\(a>1\)时\(g(a) >0\),
综上,再结合前提条件\(a >0\),得到\(a\)的取值范围为\((0,1)\)。
感悟反思:1、此时我们常常借助导函数的图像或者导函数的分子图像,来简化判断导函数的正负。这体现了数形结合的数学思想。也体现了学以致用的数学方向。2、思路点拨,碰到解不等式\(lnx>1-x\)或者\(e^x>1-x\)这样的不等式,一般用常规代数求解的方法行不通的,此时可以考虑构造函数用导数求解,或者用图像求解不等式。3、用图像求值域
【类型⑩】已知含参函数的零点个数,求参数的取值范围;方法:分离参数+导数法;或二次函数根的分布+零点存在性定理,
分析:由题目先转化为方程\(x^2+\cfrac{m}{x}-3=0\)有三个不同的实根,
分离参数得到,方程\(-m=x^3-3x(x\neq 0)\)有三个不同的实根,
令\(g(x)=x^3-3x(x\neq 0)\),用导数方法求其单调区间,为作图做准备。
令\(g'(x)=3x^2-3>0\),得到\(x<-1\)或\(x>1\);
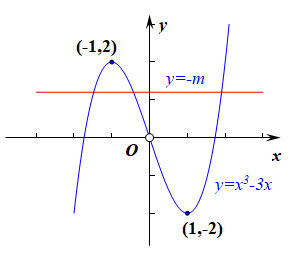
令\(g'(x)<0\),得到\(-1<x<1\),\(x\neq 0\)最后做处理。
则函数\(g(x)\)在\((-\infty,-1]\) 上单调递增,
在\([-1,1]\)上单调递减,在\([1,+\infty)\)上单调递增;
又\(g(-1)=2\),\(g(1)=-2\),手工作图如右,
在同一个坐标系中做\(y=-m\)和\(y=g(x)\)的图像,
由图像可得,\(-2<-m<2\),且\(-m\neq 0\),
解得\(m\)的取值范围为\((-2,0)\cup(0,2)\)。
感悟反思:1、分离参数法,2、数形结合思想。3、形如函数\(f(x)=g(x)-a\)有\(n\)个零点的问题,常常就转化为方程\(a=g(x)\)有\(n\)个解得问题。解法:用导数做出函数g(x)的大致图像,结合图像求解
【类型⑾】已知函数存在单调递减区间,求参数的取值范围;解法思路:转化为g'(x)<0能成立(或有解),或转化为能成立问题;
【法1,二次函数法】:\(f′(x)=\cfrac{1}{x}-ax-2=\cfrac{1-ax^2-2x}{x}\)
由题意知\(f′(x)<0\)有实数解(注意不是\(f'(x)\leq 0\)),
由于\(x>0\),
故\(ax^2+2x-1>0(a<0)\)有正的实数解.
又对称轴\(x=-\cfrac{1}{a}>0\),
故只要\(\Delta =4+4a>0\),
解得\(a>-1\),又\(a<0\)
则\(-1<a<0\);
【法2,导数法】\(f′(x)=\cfrac{1}{x}-ax-2=\cfrac{1-ax^2-2x}{x}\)
由题意知\(f′(x)<0\)在区间\((0,+\infty)\)有实数解(注意不是\(f'(x)\leq 0\)),
即\(1-ax^2-2x<0\)有正实根,
分离参数,得到\(a>\cfrac{1}{x^2}-\cfrac{2}{x}\)在区间\((0,+\infty)\)有实数解,
又当\(x>0\)时,\(\cfrac{1}{x^2}-\cfrac{2}{x}=(\cfrac{1}{x}-1)^2-1\ge -1\),
故\(a>-1\),又\(a<0\)
则\(-1<a<0\);
分析:由于函数中含有参数,所以先考虑\(g'(x)\leq 0\)在区间\((0,+\infty)\)上有解或能成立;
\(g'(x)=\cfrac{1}{x}+x-(b-1)=\cfrac{x^2-(b-1)x+1}{x}\),则只需要\(h(x)=x^2-(b-1)x+1\leq 0\)在区间\((0,+\infty)\)上有解或能成立;
分离参数得到\(b-1\ge \cfrac{x^2+1}{x}=x+\cfrac{1}{x}\)在区间\((0,+\infty)\)上有解或能成立;\([x+\cfrac{1}{x}]_{min}=2\)
故\(b-1\ge 2\),即\(b\ge 3\),注意\(b=3\)时往往需要验证,
比如此时的\(g'(x)=\cfrac{x^2-(3-1)x+1}{x}=\cfrac{(x-1)^2}{x}\),此时\(g'(x)\ge 0\)恒成立,故\(b=3\)要舍去,即\(b>3\).
感悟反思:1、注意是\(f'(x)<0\)有解,而不是\(f'(x)\leq 0\)有解,或者理解为先令\(f'(x)\leq 0\),然后验证取等号的情形。
比如此题中,当取到等号时,\(a=-1\),但此时有\(f'(x)=\cfrac{1+x^2-2x}{x}=\cfrac{(x-1)^2}{x}\ge 0\),不符合题意了,故\(a=-1\)必须舍掉。2、当转化为二次函数有解问题时,自然可以借助二次函数来求解。
【类型⑿】已知含参数\(a\)的函数\(f(x)\)有极值,求参数\(a\)的取值范围;解法思路:具体情况具体分析;
类型1:仅仅提到函数有极值;
方法思路1:\(f'(x)=0\)有解,分离参数\(a=g(x)\),转化为求\(g(x)\)的值域,但是必须排除不变号零点;不变号零点往往就是值域中的端点值;
方法思路2:由于函数有极值,则函数不单调,先求函数单调时的参数取值,再求其补集;
类型2:既提到函数有极值,且给定了极值和的范围,
方法思路:\(f'(x)=0\)有解,分离参数\(a=g(x)\),往往会转化为方程\(g(x)=0\)有两个不等正实数根,从而利用判别式和韦达定理,最后结合\(f(x_1)+f(x_2)\)与极值和的范围,求得\(a\)的取值范围;
类型3:给定了含参函数\(f(x)\)在点\(x_0\)处取到极小值,
方法思路:则\(f'(x)=0\)必有解\(x=x_0\)(必须是变号零点),且导函数\(f'(x)\)的图像必须满足在\(x_0\)处左负右正,故此时不能用分离参数的方法,必须分类讨论,当上述条件都成立的参数必然入围取值范围。
思路比较:上述的3个类型的求解思路和方程有实数根的求解很类似。比如方程有实数根,只需要限制判别式;如果有两正实数根,需要再添加限制如韦达定理;如果还给定正实数根的范围,这时就需要添加更多的条件;
【类型⒀】已知形如\(a=f(x)\)的方程有解或无解; 解法思路:转化划归为求函数\(f(x)\)的值域问题,
模型\(a=f(x)\)有解等价于求\(f(x)\)的值域(或用导数做出大致图像,得出值域),此时不排除值域的端点值;
\(a=f(x)\)无解,可以先求\(a=f(x)\)有解,再求其补集,间接法,正难则反;
【类型⒁】函数\(y=f(x)\)在某个区间\((a,b)\)单调(或不单调),求参数的取值范围;
解法思路:转化为恒成立命题,或利用补集思想
A.\([0,+\infty)\) \(\hspace{1cm}\) B.\((-\infty,0]\) \(\hspace{1cm}\) C. \((-\infty,0)\) \(\hspace{1cm}\) D. \((0,+\infty)\) ;
分析:由题意知\(x>0\),又\(f′(x)=1+\cfrac{a}{x}\),
要使函数\(f(x)=x+alnx\)不是单调函数,
则需方程\(1+\cfrac{a}{x}=0\;\)在\(x>0\)上有解,
即方程\(a=-x\)在\(x>0\;\)上有解,
又函数\(g(x)=-x\)在\(x>0\)上的值域是\((-\infty,0)\),故\(a\in(-\infty,0)\)。
\(\fbox{又例}\)(不是单调递减)
已知函数\(f(x)=-\cfrac{1}{3}x^3+bx^2-(2b+3)x+2-b\;\;\)在\(R\)上不是单调递减函数,则\(b\)的取值范围是___________。
分析:若是\(R\)上的单调递减函数,则\(f'(x)\leq 0\;\;\)恒成立,
现在不是R上的单调递减函数,
故\(f'(x)=-x^2+2bx-2b-3=-(x-b)^2+b^2-2b-3>0\;\;\)在\(R\)上能成立,
故只需要\(f'(x)_{max}=b^2-2b-3>0\;\)即可,
解得\(b<-1\)或\(b>3\)。故\(b\in (-\infty,-1)\cup(3,+\infty)\)。
反思总结:不是单调递减的情形可能包含有单调递增函数或常函数或有增有减函数。
\(\fbox{又例}\)(函数不单调)
函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\;\)在区间\([-1,2]\)上不单调,则实数\(a\)的取值范围是_________。
法1:补集思想,\(f'(x)=x^2-2x+a\),
若函数\(f(x)\)在\([-1,2]\)上单增,则\(f'(x)=x^2-2x+a\ge 0\;\;\)恒成立,
分离参数得到\(a\ge -x^2+2x\)恒成立,
在\([-1,2]\)上求得函数\(f(x)_{max}=1\),故\(a\ge 1\);
若函数\(f(x)\)在\([-1,2]\)上单减,则\(f'(x)=x^2-2x+a\leq 0\;\;\)恒成立,
分离参数得到\(a\leq -x^2+2x\)恒成立,
在\([-1,2]\)上求得函数\(f(x)_{min}=-3\),故\(a\leq -3\);
故取其补集,当\(-3< a <1\)时,函数\(f(x)\)在区间\([-1,2]\)上不单调。
法2:由题可知\(f(x)\)不单调,
则导函数\(y=f'(x)\)在区间\([-1,2]\)上至少有一个变号零点,
当只有一个变号零点时,
由\(f'(-1)\cdot f'(2)\leq 0\)可得,\(-3\leq a\leq 0\);
当有两个变号零点时,
由\(\begin{cases}f'(-1)>0\\f'(2)>0\\\Delta >0\end{cases}\),
解得\(0< a <1\);
综上所述,实数\(a\)的取值范围是\((-3,1)\)。
二、中档题型和解法
【类型①】求函数的最值中出现了二阶导;
解法思路:二阶导的正负能判断一阶导的增减性,一阶导的单调性和端点值能判断原函数的增减性
(2)、求函数\(f(x)\)在区间\([0,\cfrac{\pi}{2}]\)上的最大值和最小值。
分析:(1)由题目可知,\(f'(x)=e^xcosx+e^x\cdot (-sinx)-1=e^x(cosx-sinx)-1\)
则切线的斜率\(k=f'(0)=e^0(cos0-sin0)-1=0\),
又\(f(0)=(e^xcosx-x)_{|x=0}=1\),即切点为\((0,1)\),
由点斜式可知切线方程为\(y-1=0(x-0)\),
整理得到在点\((0,f(0))\)处的切线方程为\(y=1\)。
(2)由上可知,\(f'(x)=e^x(cosx-sinx)-1\),
令\(h(x)=e^x(cosx-sinx)-1\),
则\(h'(x)=e^x(cosx-sinx)+e^x(-sinx-cosx)=-2e^xsinx\),
当\(x\in (0,\cfrac{\pi}{2})\)时, 容易知道\(h'(x)=-2e^xsinx<0\)(注意恒有\(e^x>0\)),
即函数\(h(x)\),也就是函数\(f'(x)\),在\(x\in (0,\cfrac{\pi}{2})\)单调递减,
则\(x\in [0,\cfrac{\pi}{2}]\)时,\(h(x)\leq h(0)=0\),即$f'(x)\leq 0 $恒成立,
即使\(f'(x)=0\),也是仅仅在单独的端点处,不会影响函数\(f(x)\)的单调性。
则有函数\(f(x)\)在区间$ [0,\cfrac{\pi}{2}]$上单调递减,
故\(f(x)_{min}=f(\cfrac{\pi}{2})=-\cfrac{\pi}{2}\),\(f(x)_{max}=f(0)=1\)。
感悟反思:
1、关于二阶导的那些事,由解答过程就能看出,函数\(h(x)\)是函数\(f(x)\)的一阶导数,那么函数\(h'(x)\)其实是函数\(f(x)\)的二阶导,由于高中阶段我们只接触学习了一阶导数,故答案中一般不出现二阶导\(f''(x)\)的表示形式,我们做答案是也需要注意这一点。
2、为什么要用二阶导?平时我们的解题经验是一般只给函数\(f'(x)\)求一次导数得到\(f'(x)\),然后求解导函数不等式,由导函数的正负就知道了原函数\(f(x)\)的单调性了;
但是,不是所有的函数求一阶导后,导函数的正负我们就能一目了然,这时候往往需要针对导函数再求导,也就是二阶导,其目的就是想知道导函数的单调性,
在我们的解题体验中,往往是二阶导恒为正或恒为负,这样我们就知道了一阶导的单调性,利用一阶导的端点值(往往为0),从而知道了一阶导的正负,
这样原函数的单调性就清楚了。
3、由于上述比较拗口,结合题目做以说明。原函数为\(f(x)\),一阶导为\(f'(x)=h(x)\),二阶导为\(h'(x)=f''(x)\),
由于二阶导\(h'(x)=f''(x)=-2e^xsinx<0\)在\((0,\cfrac{\pi}{2})\)上恒成立,则一阶导\(h(x)=f'(x)\)在\([0,\cfrac{\pi}{2}]\)上单调递减;
此时一阶导\(h(x)=f'(x)\)有最值,取哪一个最值,一般取函数值为0的那一个。比如\(h(x)_{max}=h(0)=0\),
从而知道一阶导\(f'(x)<0\),这样就知道了原函数\(f(x)\)在\([0,\cfrac{\pi}{2}]\)上单调递减;
接下来求最值,那还不是小菜一碟吗。
【类型②】已知绝对值函数不等式,求参数的取值范围;
解法思路:利用单调性去掉绝对值符号,重新构造函数,将问题转化为其他可以求解的类型
分析:先求定义域得\((0,+\infty)\),求导得到\(f'(x)=\cfrac{a+1}{x}+2ax=\cfrac{2ax^2+a+1}{x}\),
然后只考虑分子函数\(g(x)=2ax^2+a+1\)的图像,
先考虑\(a=0\),在考虑函数\(g(x)\)图像恒在\(x\)轴上方,恒在\(x\)轴下方,以及\(x\)轴上方下方都有图像的情形,
自然就得到了分类的标准有\(a=0\),\(a>0\),\(a+1\leq 0\),以及\(-1< a<0\),在解答时做一综合就行了。
解:当\(a\ge 0\)时,\(g(x)>0\)恒成立,则\(f'(x)=\cfrac{2ax^2+a+1}{x}>0\),故\(f(x)\)在\((0,+\infty)\)上单调递增;
当\(a\leq -1\)时,\(g(x)\leq 0\)恒成立,则则\(f'(x)=\cfrac{2ax^2+a+1}{x}<0\),故\(f(x)\)在\((0,+\infty)\)上单调递减;
当\(-1< a<0\)时,令\(f'(x)=0\),解得\(x=\sqrt{-\cfrac{a+1}{2a}}=x_0\),即\(x\in(0,x_0)\)时,\(f'(x)>0\),
故\(f(x)\)在\((0,x_0)\)上单调递增;\(x\in(x_0,+\infty)\)时,\(f'(x)<0\),故\(f(x)\)在\((x_0,+\infty)\)上单调递减;
(2)设\(a<-1\),若对任意\(x_1,x_2\in(0,+\infty)\),恒有\(|f(x_1)-f(x_2)|\ge 4|x_1-x_2|\),求\(a\)的取值范围。
不妨设\(x_1\leq x_2\),由(1)可知,\(a<-1\)时\(f(x)\)在\((0,+\infty)\)单调递减,
从而对任意\(x_1,x_2\in(0,+\infty)\),恒有\(|f(x_1)-f(x_2)|\ge 4|x_1-x_2|\),
可以等价转化为\(f(x_1)-f(x_2)\ge 4(x_2-x_1)\),
即任意\(x_1,x_2\in(0,+\infty)\),恒有\(f(x_1)+4(x_1)\ge f(x_2)+4x_2\),
【到此,构造函数就有了依托】
令\(g(x)=f(x)+4x\),则\(x_1\leq x_2\),\(g(x_1)\ge g(x_2)\)原命题等价于函数\(g(x)\)在\((0,+\infty)\)上单调递减。
而\(g'(x)=\cfrac{a+1}{x}+2ax+4=\cfrac{2ax^2+4x+a+1}{x}\leq 0\)在\((0,+\infty)\)上恒成立。
接下来的思路就比较多了:
思路1:分离参数法,
\(a\leq \cfrac{-4x-1}{2x^2+1}=\cfrac{(2x-1)^2-4x^2-2}{2x^2+1}=\cfrac{(2x-1)^2}{2x^2+1}-2\),
故\(a\leq -2\)。
思路2:只关注导函数\(g'(x)\)的分子,
令\(h(x)=2ax^2+4x+a+1\),则转化为\(h(x)\leq 0\)在\((0,+\infty)\)上恒成立,
分离参数得到,\(a\leq (\cfrac{-4x-1}{2x^2+1})_{min}\),
令\(\phi(x)=\cfrac{-4x-1}{2x^2+1}\),
解得\(\phi'(x)=\cfrac{-4(2x^2+1)-(-4x-1)\cdot 4x}{(2x^2+1)^2}\)
\(=\cfrac{8x^2+4x-4}{(2x^2+1)^2}=\cfrac{4(2x-1)(x+1)}{(2x^2+1)^2}\),
故\(x\in(0,\cfrac{1}{2})\)时,\(\phi'(x)<0\),\(\phi(x)\)单调递减,
\(x\in(\cfrac{1}{2},+\infty)\)时,\(\phi'(x)>0\),\(\phi(x)\)单调递增,
故\(\phi(x)_{min}=\phi(\cfrac{1}{2})=-2\),故\(a\leq -2\)。
思路3:只关注导函数\(g'(x)\)的分子,令\(h(x)=2ax^2+4x+a+1\),
则转化为\(h(x)\leq 0\)在\((0,+\infty)\)上恒成立,利用二次函数求解。
则\(\begin{cases}h(0)\leq 0\\x=-\cfrac{4}{2\times 2a}<0\\ \Delta >0\end{cases}\)或者$ \Delta \leq 0$,
解得\(a\leq -2或a\ge 1\),又\(a<-1\),故\(a\leq -2\)。
思路4:接思路1,分离参数得到,\(a\leq \cfrac{-4x-1}{2x^2+1}\),
求函数\(\phi(x)=\cfrac{-4x-1}{2x^2+1}\)的最小值,
还可以用代换法,令\(-4x-1=t<-1\),
则\(\phi(x)=\cfrac{t}{\cfrac{(t+1)^2}{8}+1}\)
\(=\cfrac{8t}{t^2+2t+9}=\cfrac{8}{t+\cfrac{9}{t}+2}\ge \cfrac{8}{-2\sqrt{9}+2}=-2\),
故\(a\leq -2\)。
感悟反思:1、第一问的结果为第二问去掉绝对值做准备。2、利用单调性去掉绝对值,然后重新整理得到一个左右结构相同的不等式,这样就可以构造函数了。
三、难点题型和解法
用导数证明不等式,构造函数,常用的不等关系 极值点偏移问题
【类型①】给定恒成立能成立命题,求参数的取值范围;解法思路:先分别解决恒成立和能成立问题,再转化划归解不等式问题;
⑵讨论函数\(f(x)\)在\([-\pi,\pi]\)上的单调性;
⑶设函数\(g(x)=xlnx+\cfrac{m}{x}\),若对任意的\(x_1\in[\cfrac{1}{2},2]\)总存在\(x_2\in[0,\cfrac{\pi}{2}]\),使得\(g(x_1)\ge f(x_2)\)成立,求实数\(m\)的取值范围。
分析:⑴利用\(f'(x_0)=f'(\cfrac{\pi}{4})=\cfrac{\sqrt{2}\pi}{8}\),求得\(a=1\);
⑵利用解不等式\(f'(x)>0\)得到单调区间或者利用两个函数\(y=x\),\(y=cosx\),
\(x\in[-\pi,\pi]\)的图像直接写出单调区间;课件
⑶由题目可知\(\forall x_1\in [\cfrac{1}{2},2]\),\(\exists x_2\in [0,\cfrac{\pi}{2}]\),使得\(g(x_1)\ge f(x_2)\)成立,
即就是\(g(x_1)_{min}\ge f(x_2)_{max}\),且\(x_1\in [\cfrac{1}{2},2]\),\(x_2\in [0,\cfrac{\pi}{2}]\)。
接下来求解函数\(g(x_1)\)在\(x_1\in [\cfrac{1}{2},2]\)上的最小值,
再求解函数\(f(x_2)\)在\(x_2\in [0,\cfrac{\pi}{2}]\)上的最大值,
再代入上述的不等式求解得到实数\(m\)的取值范围。
【类型②】已知恒成立+隐含构造函数,求参数的取值范围;解法思路:观察条件构造函数,转化为恒成立命题处理;
⑴令\(F(x)=x\cdot f(x)-g(x)\),求\(F(x)\)的单调区间;
⑵若任意\(x_1,x_2\in [1,+\infty)\),且\(x_1>x_2\),都有\(m[g(x_1)-g(x_2)]>x_1f(x_1)-x_2f(x_2)\)恒成立,求实数\(m\)的取值范围;
分析:⑴由于\(g(x)\)是分段函数,故按道理求\(F(x)\) 也应该是分段函数,
但是\(f(x)\)的定义域是\((0,+\infty)\),故\(F(x)\)也应该定义在\((0,+\infty)\)上,
故\(F(x)=xlnx-\cfrac{1}{2}x^2\),则\(F'(x)=lnx+1-x=lnx-(x-1)=f(x)-h(x)\)
到此可以考虑两个思路:
其一,利用函数\(y=f(x)\)和\(h(x)=x-1\)的图像很快的看出\(F'(x)\)的正负, 课件
课件
故当\(0< x <1\)时,\(F'(x)<0\);当\(x >1\)时,\(F'(x)<0\);当\(x=1\)时,\(F'(x)=0\);
即\(x\in (0,+\infty)\)时,\(F'(x)\leq 0\)恒成立,即函数\(F(x)\)只有单调递减区间\((0,+\infty)\)。
其二:构造函数\(G(x)=F'(x)=lnx+1-x\),则\(G'(x)=\cfrac{1}{x}-1\),
由\(G'(x)=\cfrac{1}{x}-1>0\),得到\(0< x <1\);由\(G'(x)=\cfrac{1}{x}-1<0\),得到\(x >1\);
即\(G(x)\)在\((0,1)\)上为增函数,在\((1,+\infty)\)上为减函数,即\(F'(x)\)在\((0,1)\)上为增函数,
在\((1,+\infty)\)上为减函数,故\(F'(x)\leq F'(1)=0\),故函数\(F(x)\)在区间\((0,+\infty)\)上单调递减。
⑵由题意当\(x_1> x_2\ge 1\)时,都有\(m[g(x_1)-g(x_2)]>x_1f(x_1)-x_2f(x_2)\)恒成立,
故当\(x_1 >x_2\ge 1\)时,\(mg(x_1)-x_1f(x_1)>mg(x_2)-x_2f(x_2)\)恒成立,
此时构造函数\(H(x)=mg(x)-xf(x)\),则函数\(H(x)\)在区间\([1,+\infty)\)上是增函数,
则有\(H'(x)\ge 0\)恒成立;又\(H(x)=m\cfrac{1}{2}x^2-xlnx\),则\(H'(x)=mx-lnx-1\ge 0\)恒成立,分离参数得到
\(m\ge \cfrac{lnx+1}{x}\),再令\(h(x)=\cfrac{lnx+1}{x}(x\ge 1)\),
则\(h'(x)=\cfrac{1-lnx-1}{x^2}=\cfrac{-lnx}{x^2}\leq 0\),故\(h(x)\)在\([1,+\infty)\)上单调递减;故\(h(x)_{max}=h(1)=1\),故\(m\ge 1\)。
【类型③】已知方程根的个数,求参数的取值范围;证明不等式
(1)讨论\(f(x)\)的单调性;
分析:利用导数求导解决,
\(f'(x)=e^x(e^x-a)+e^x\cdot e^x-a^2=\)\(2e^{2x}-e^xa-a^2=(e^x-a)\cdot (2e^x+a)\),
以下针对\(a\)分类讨论如下:
当\(a=0\)时,\(f'(x)>0\)恒成立,\(f(x)\)在区间\((-\infty,+\infty)\)上单调递增。
当\(a >0\)时,令\(f'(x)=0\),解得\(x=lna\),
则\(x\in(-\infty,lna)\)时,\(f'(x)<0\),即在区间\((-\infty,lna)\)上函数\(f(x)\)单调递减;
\(x\in(lna,+\infty)\)时,\(f'(x)>0\),即在区间\((lna,+\infty)\)上函数\(f(x)\)单调递增;
当\(a <0\)时,令\(f'(x)=0\),解得\(x=ln(-\cfrac{a}{2})\),
则\(x\in(-\infty,ln(-\cfrac{a}{2})\)时,\(f'(x)<0\),即在区间\((-\infty,ln(-\cfrac{a}{2}))\)上函数\(f(x)\)单调递减;
\(x\in(ln(-\cfrac{a}{2}),+\infty)\)时,\(f'(x)>0\),即在区间\((ln(-\cfrac{a}{2}),+\infty)\)上函数\(f(x)\)单调递增;
综上所述,
当\(a<0\)时,函数\(f(x)\)的单减区间是\((-\infty,ln(-\cfrac{a}{2}))\),单增区间是\((ln(-\cfrac{a}{2}),+\infty)\);
当\(a=0\)时,单增区间是\((-\infty,+\infty)\),无单减区间;
当\(a>0\)时,函数\(f(x)\)的单减区间是\((-\infty,lna)\),单增区间是\((lna,+\infty)\);
【类型④】证明不等式;
解法思路:构造函数,用导数证明不等式,
(1)讨论函数\(f(x)\)的单调性。
(2)当\(x>y>e-1\)时,证明不等式\(e^x\cdot ln(1+y)>e^y\cdot ln(1+x)\)
分析:(1)定义域为\((0,+\infty)\),又\(f'(x)=a-\cfrac{1}{x}=\cfrac{ax-1}{x}\),
由于分母为正,故只针对分子\(ax-1\)分类讨论,
当\(a\leq 0\)时,\(ax-1<0\),即\(f'(x)<0\),故在\((0,+\infty)\)上单调递减;
当\(a>0\)时,令\(ax-1=0\),得到\(x=\cfrac{1}{a}\),
故在\((0,\cfrac{1}{a})\)上单调递减,在\((\cfrac{1}{a},+\infty)\)上单调递增。
(2)将欲证明结论\(e^x\cdot ln(1+y)>e^y\cdot ln(1+x)\)变形为\(\cfrac{ln(1+y)}{e^y}>\cfrac{ln(1+x)}{e^x}\),
题目转化为由\(x>y>e-1\)时,证明\(\cfrac{ln(1+y)}{e^y}>\cfrac{ln(1+x)}{e^x}\),
故我们构造函数\(g(x)=\cfrac{ln(1+x)}{e^x}\),
这样命题转化为当\(x>y>e-1\)时,\(g(y)>g(x)\),
故只需要证明函数\(g(x)\)在\((e-1,+\infty)\)上单调递减即可。
以下用导数证明。
\(g'(x)=\cfrac{\cfrac{1}{x+1}\cdot e^x-ln(x+1)\cdot e^x}{(e^x)^2}=\cfrac{\cfrac{1}{x+1}-ln(x+1)}{e^x}\),
令\(h(x)=\cfrac{1}{x+1}-ln(x+1)\),
则\(h'(x)=-\cfrac{1}{(x+1)^2}-\cfrac{1}{x+1}=-\cfrac{x+2}{(1+x)^2}\),
当\(x>e-1\)时,很显然\(h'(x)<0\);
故函数\(h(x)\)在\((e-1,+\infty)\)上单调递减,
故\(h(x)<h(e-1)=\cfrac{1}{e}-1<0\),
故导函数\(g'(x)=\cfrac{h(x)}{e^x}<0\)在\((e-1,+\infty)\)上恒成立,
故函数\(g(x)\)在\((e-1,+\infty)\)上单调递减,
证毕。


 函数与导数部分的题型梳理
函数与导数部分的题型梳理
